Product of Array Except Self - LeetCode #238

Being one of the most asked questions and also one of the important problem patterns on LeetCode, the product of array except self problem has become a subject of interest for this blog. It uses a modification of a general approach called prefix sum as an optimal solution.

Let’s dive into it!

Problem Statement

You can find the problem statement here: Product of Array except Self - LeetCode

Solution(s)

1. Naive Approach - Brute Force

The brute-force approach to solution is simple. For each index in the the array, we calculate the product of every remaining element.

The python code for it will look like this:

def productExceptSelf(nums):
    n = len(nums)
    result = [0]*n
    for i in range(n):
        product = 1
        for j in range(n):
            if i != j:
                product = product * nums[j]
        result[i] = product
    return result

Time Complexity: O(N2)
Space Complexity: O(1) [Not considering the result array]

2. Better Approach - Prefix and postfix products

As we can observe in the brute-force solution, there is a lot of recomputation happening which can be avoided to speed up our code. All we have to do is to precompute all the products from the left side and right side leaving apart the element at their index and have 2 new arrays holding the products. We can do this in two single passes through the array and then we can finally make the result array going through the arrays once more. A more detailed explanation can be seen in the image below:

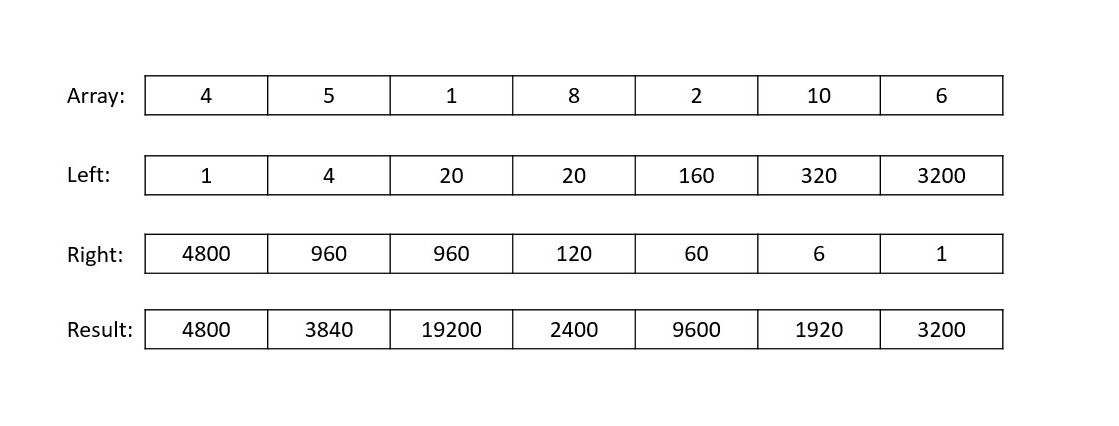
The time complexity will be reduced to O(N) due to single passes but the space complexity will rise to be O(N) as well.

The python code for this approach is given below:

def productExceptSelf(nums):
    n = len(nums)
    left_prod = [1] * n
    right_prod = [1] * n
    result = [1] * n

    for i in range(1, n):
        left_prod[i] = left_prod[i-1] * nums[i-1]
        
    for i in range(n-2, -1, -1):
        right_prod[i] = right_prod[i+1] * nums[i+1]
    
    for i in range(n):
        result[i] = left_prod[i] * right_prod[i]

    return result

Time Complexity: O(N)
Space Complexity: O(N) [Extra space used for Left Product and Right Product arrays]

3. Optimal Approach - Prefix and postfix products without extra space

We can modify the approach discussed above to not use any extra space by simple trickery.

The python code for it is given below:

def productExceptSelf(nums):
    n = len(nums)
    result = [1] * n

    for i in range(1, n):
        result[i] = result[i-1] * nums[i-1]
        
    r_prod = 1

    for i in range(n-1, -1, -1):
        result[i] = r_prod * result[i]
        r_prod *= nums[i]

    return result

Time Complexity: O(N)
Space Complexity: O(1) [Extra space not used - Disregarding result array]

Best of Luck! Later.